Polynomials are mathematical expressions that involve variables raised to non-negative integer powers, combined with various coefficients and mathematical operations. Solving polynomials is a fundamental skill in algebra, and it forms the basis for solving a wide range of mathematical problems. In this article, we will explore the process of Solving Polynomials, step-by-step. We’ll also provide a detailed example to illustrate the concepts.
Step 1: Understanding Polynomials
Before diving into solving polynomials, it’s important to understand what they are. A polynomial is an algebraic expression consisting of terms, each of which has a coefficient and an exponent. For example, \(3x^2 – 5x + 2\) is a polynomial in the variable \(x\), where \(3\), \(-5\), and \(2\) are coefficients, and \(x^2\), \(x\), and the constant \(2\) are terms.
Step 2: Identifying the Polynomial Degree
The degree of a polynomial is determined by the highest exponent of the variable present in the polynomial. This is crucial because it helps us understand the behavior and characteristics of the polynomial. For instance, in the polynomial \(3x^2 – 5x + 2\), the highest exponent is \(2\), so the degree of the polynomial is \(2\), making it a quadratic polynomial.
Step 3: Factoring the Polynomial (if possible)
Factoring a polynomial involves breaking it down into simpler terms, which can often reveal its roots or solutions. The roots of a polynomial are the values of the variable that make the polynomial equal to zero. Let’s consider an example to illustrate this process:
Example: Solve the quadratic polynomial \(x^2 – 5x + 6\) using factoring.
Solution:
1. Start with the polynomial: \(x^2 – 5x + 6\).
2. Try to factor the polynomial by finding two numbers whose product is the product of the coefficient of the quadratic term (\(1\)) and the constant term (\(6\)) and whose sum is the coefficient of the linear term (\(-5\)).
– The numbers \(2\) and \(3\) satisfy these conditions: \(2 \times 3 = 6\) and \(2 + 3 = 5\).
3. Rewrite the middle term (\(-5x\)) using the factored numbers: \(x^2 – 2x – 3x + 6\).
4. Group the terms: \(x(x – 2) – 3(x – 2)\).
5. Factor out the common term \((x – 2)\): \((x – 2)(x – 3)\).
6. Set each factor equal to zero and solve for \(x\): \(x – 2 = 0\) or \(x – 3 = 0\).
7. Solve for \(x\): \(x = 2\) or \(x = 3\).
Step 4: Using the Quadratic Formula
In cases where factoring isn’t possible or practical, the quadratic formula is a powerful tool for solving quadratic polynomials. The quadratic formula states that for a quadratic polynomial of the form \(ax^2 + bx + c = 0\), the solutions for \(x\) are given by:
\[x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\]
Where \(a\), \(b\), and \(c\) are the coefficients of the quadratic polynomial. Let’s apply the quadratic formula to an example:
Example: Solve the quadratic polynomial \(2x^2 – 7x + 3\) using the quadratic formula.
Solution:
1. Start with the polynomial: \(2x^2 – 7x + 3\).
2. Identify the coefficients: \(a = 2\), \(b = -7\), and \(c = 3\).
3. Apply the quadratic formula:
\[x = \frac{-(-7) \pm \sqrt{(-7)^2 – 4 \cdot 2 \cdot 3}}{2 \cdot 2}\]
4. Simplify the formula:
\[x = \frac{7 \pm \sqrt{49 – 24}}{4}\]
\[x = \frac{7 \pm \sqrt{25}}{4}\]
5. Continue simplifying:
\[x = \frac{7 \pm 5}{4}\]
6. Solve for both values of \(x\):
\[x_1 = \frac{7 + 5}{4} = 3\]
\[x_2 = \frac{7 – 5}{4} = \frac{1}{2}\]
Step 5: Handling Higher-Degree Polynomials
For polynomials of degree higher than \(2\), factoring and the quadratic formula may not be sufficient. In such cases, we can use numerical methods like the Rational Root Theorem, synthetic division, or graphing to approximate solutions. Additionally, some higher-degree polynomials may have special properties that aid in finding solutions.
Solving polynomials is a crucial skill in algebra and lays the foundation for solving a variety of mathematical problems. By understanding the degree of the polynomial, factoring, using the quadratic formula, and employing other numerical methods, students can effectively find the solutions to polynomial equations. Whether the polynomial is linear, quadratic, or higher-degree, each type requires a unique approach to find its solutions. Armed with these techniques, students can confidently tackle a wide range of polynomial equations and gain a deeper appreciation for the beauty and complexity of mathematics.
In this article, we’ve explored the step-by-step process of solving polynomials. We’ve covered the fundamentals, demonstrated factoring and quadratic formula methods with examples, and touched on how to approach higher-degree polynomials. Through practice and understanding, students can master polynomial solving and develop essential problem-solving skills that extend to various mathematical and scientific disciplines. Remember, mathematics is not just about finding answers; it’s about the journey of exploration, discovery, and critical thinking. Use maths.ai to unlock your mathematical journey.
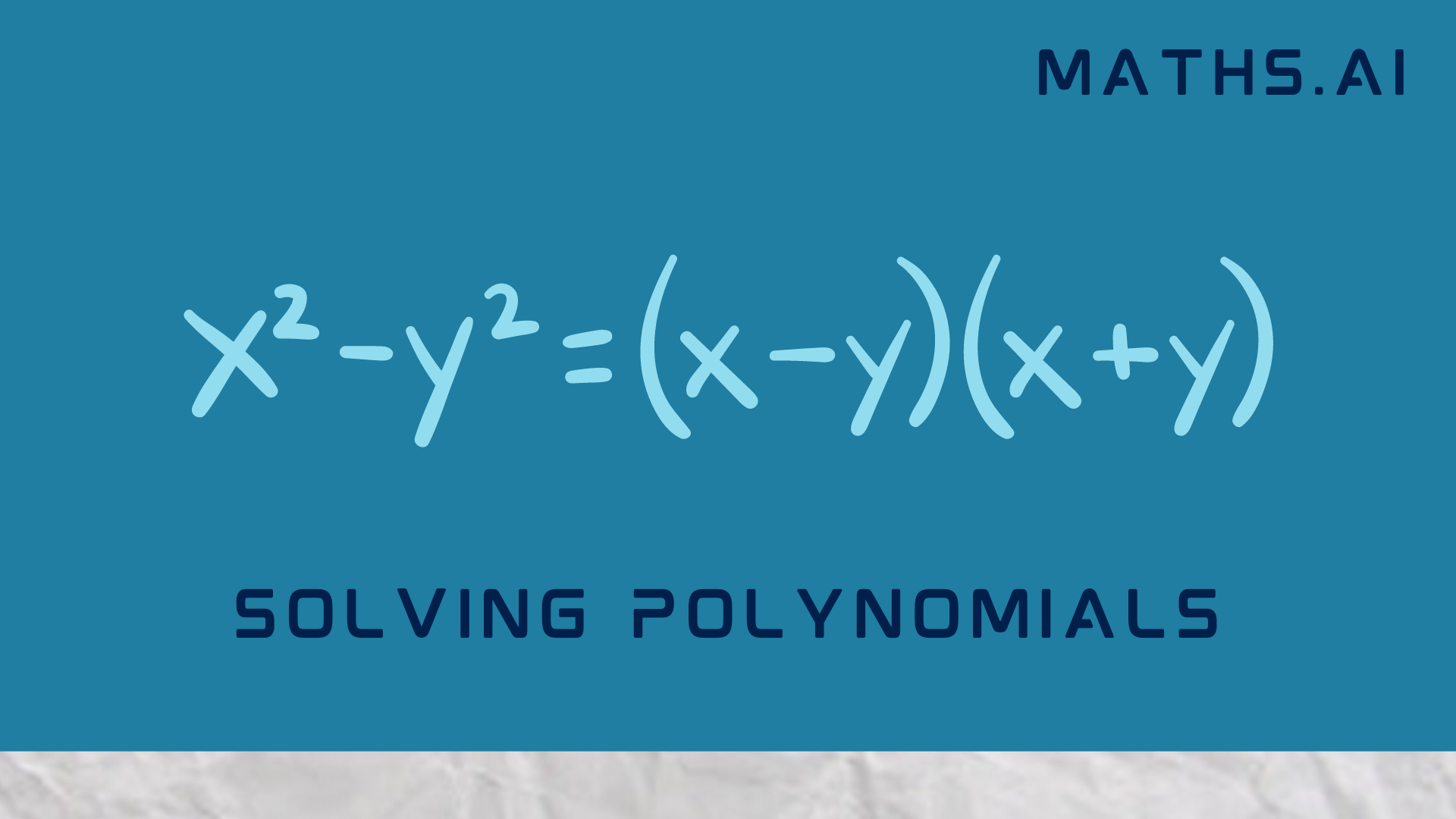


One Comment